7 Fundamentos de la Inferencia Estadística

El mundo moderno genera cantidades masivas de datos día tras día. Sin embargo, ¿de qué sirve acumular información si no podemos extraer conocimiento valioso de ella? Aquí es donde entra en juego una de las herramientas más poderosas del análisis cuantitativo: la Inferencia Estadística.

Imagina poder tomar decisiones fundamentadas sobre una población completa examinando solo una pequeña fracción de ella. No es magia, es matemática aplicada en su forma más elegante y práctica. Los profesionales que dominan estas técnicas poseen una ventaja competitiva significativa en campos tan diversos como la medicina, la economía y la investigación científica. ¿Estás listo para adentrarte en este fascinante universo de probabilidades, muestras y estimaciones? La puerta hacia un nuevo nivel de comprensión analítica está a punto de abrirse.

Inferencia Estadística

La Inferencia Estadística constituye el corazón metodológico de las ciencias cuantitativas, permitiéndonos realizar el salto cognitivo desde lo particular hacia lo general. En términos técnicos, se define como el conjunto de métodos y procedimientos que posibilitan extraer conclusiones válidas sobre los parámetros de una población a partir del análisis de una muestra representativa de la misma.

¿Pero qué implica esto realmente? Cuando un farmacólogo prueba un medicamento en 500 pacientes para determinar su eficacia en millones de potenciales usuarios, está aplicando inferencia estadística. Cuando un politólogo encuesta a 1,200 votantes para predecir el resultado de unas elecciones nacionales, recurre a estos mismos principios.

La belleza de esta disciplina radica en su capacidad para cuantificar la incertidumbre inherente a sus propias conclusiones. No solo nos proporciona estimaciones, sino también los márgenes de error y niveles de confianza asociados a dichas estimaciones. Esta transparencia matemática representa una de sus mayores fortalezas.

La inferencia estadística se fundamenta en la teoría de la probabilidad y emplea herramientas como intervalos de confianza, pruebas de hipótesis, estimación puntual y estimación por intervalos. Su desarrollo histórico ha sido paralelo al avance científico, convirtiéndose en un pilar indispensable para la investigación empírica contemporánea.

En la era del big data, paradójicamente, su relevancia no ha disminuido sino aumentado. Ante conjuntos de datos inabarcables en su totalidad, los métodos inferenciales nos ofrecen aproximaciones eficientes y matemáticamente justificadas. La diferencia es que ahora podemos trabajar con muestras mayores y técnicas computacionales más sofisticadas, lo que incrementa la precisión de nuestras inferencias.

Qué es la Inferencia Estadística

La Inferencia Estadística puede conceptualizarse como el puente metodológico que conecta lo conocido con lo desconocido en el universo de los datos. Formalmente, constituye la rama de la estadística dedicada a desarrollar métodos para generalizar desde observaciones particulares (muestras) hacia enunciados más amplios (sobre poblaciones) dentro de márgenes de error calculables.

Esta disciplina opera bajo el principio fundamental de que las características de una muestra adecuadamente seleccionada reflejarán, con una precisión determinable, las características de la población de la cual proviene. La clave está en la palabra «adecuadamente»: no cualquier conjunto de observaciones permite realizar inferencias válidas.

Los estadísticos distinguen entre dos grandes enfoques inferenciales:

1. La inferencia frecuentista: Basada en la noción de que los parámetros poblacionales son valores fijos desconocidos, y la probabilidad se interpreta como la frecuencia relativa de un evento en un gran número de repeticiones.
2. La inferencia bayesiana: Fundamentada en la actualización de creencias previas (distribuciones a priori) mediante la incorporación de nueva evidencia empírica, donde los parámetros se consideran variables aleatorias.

¿Cuál es la aplicación más común de la inferencia estadística? Sin duda, la estimación de parámetros poblacionales como la media, la proporción, la varianza o las correlaciones. Esto se realiza mediante estimadores puntuales (un único valor) o por intervalos (un rango de valores con un nivel de confianza asociado).

La validez de cualquier proceso inferencial depende críticamente de supuestos como la aleatoriedad en la selección muestral, la independencia de las observaciones y, frecuentemente, la normalidad en la distribución de los datos o de los estadísticos empleados.

En contextos prácticos, la inferencia estadística responde preguntas como: ¿Es efectivo este nuevo tratamiento médico? ¿Existe discriminación salarial por género en esta industria? ¿Cuál es el porcentaje de votantes que apoya determinada política pública? La potencia de estas respuestas reside en su capacidad para cuantificar la incertidumbre asociada a ellas.

Características de la Inferencia Estadística

La Inferencia Estadística posee características distintivas que la convierten en una metodología única dentro de las ciencias cuantitativas. Comprender estas propiedades resulta fundamental para aplicarla correctamente y evaluar críticamente sus resultados.

Una de sus características esenciales es su naturaleza probabilística. A diferencia de la lógica deductiva que produce conclusiones absolutamente ciertas a partir de premisas verdaderas, la inferencia estadística genera conclusiones probables, cuantificando explícitamente el nivel de incertidumbre. Esta característica no constituye una debilidad sino una fortaleza: reconoce honestamente las limitaciones inherentes al razonamiento inductivo.

Otra propiedad fundamental es su dependencia de la teoría del muestreo. La calidad de cualquier inferencia está íntimamente ligada a la representatividad de la muestra utilizada. Una muestra sesgada producirá invariablemente conclusiones erróneas, independientemente de la sofisticación del análisis posterior. Por ello, el diseño muestral constituye un paso crítico en todo proceso inferencial.

La inferencia estadística también se caracteriza por su dualidad metodológica. Proporciona tanto herramientas para la estimación de parámetros (intervalos de confianza, estimadores puntuales) como para la contrastación de hipótesis (pruebas de significación, valores p). Estas aproximaciones, aunque conceptualmente distintas, son complementarias en la práctica investigadora.

Una característica particularmente valiosa es su aplicabilidad universal. Los métodos inferenciales trascienden disciplinas específicas, siendo igualmente útiles en medicina, economía, psicología o ingeniería. Esta versatilidad explica su omnipresencia en la investigación científica contemporánea.

La inferencia estadística también posee una dimensión epistemológica relevante: establece estándares explícitos para considerar cuándo la evidencia empírica es suficiente para rechazar o aceptar provisionalmente una hipótesis. Estos criterios, aunque convencionales, proporcionan un marco común para la evaluación del conocimiento científico.

Finalmente, cabe destacar su naturaleza autocorrectiva. La inferencia estadística incluye mecanismos para detectar violaciones de sus propios supuestos y para valorar la robustez de sus conclusiones mediante análisis de sensibilidad y técnicas de diagnóstico.

Fundamentos Matemáticos de la Inferencia Estadística

Los cimientos matemáticos de la Inferencia Estadística se asientan sobre la teoría de la probabilidad, el álgebra matricial y el análisis matemático. Estas estructuras formales proporcionan el rigor necesario para desarrollar métodos inferenciales válidos y comprender sus limitaciones inherentes.

El teorema central del límite constituye uno de los pilares más importantes. Este teorema establece que, independientemente de la distribución original de una variable, la distribución de las medias muestrales se aproxima a una distribución normal conforme aumenta el tamaño muestral. ¿Por qué resulta esto tan relevante? Porque permite establecer propiedades distribucionales de los estadísticos muestrales, facilitando la construcción de intervalos de confianza y pruebas de hipótesis incluso cuando desconocemos la distribución poblacional subyacente.

Las distribuciones de probabilidad juegan un papel fundamental como modelos matemáticos que describen el comportamiento aleatorio de diversos fenómenos. Distribuciones como la normal, t de Student, chi-cuadrado, F de Snedecor o binomial constituyen herramientas indispensables para la inferencia. Cada una tiene propiedades específicas que las hacen adecuadas para diferentes contextos inferenciales.

La teoría de la estimación establece las propiedades deseables de los estimadores: insesgadez, eficiencia, consistencia y suficiencia. Un estimador insesgado tiene una esperanza matemática igual al parámetro que intenta estimar; uno eficiente presenta la menor varianza posible entre todos los estimadores insesgados; la consistencia implica que el estimador converge en probabilidad al valor real del parámetro cuando aumenta el tamaño muestral; y la suficiencia significa que el estimador incorpora toda la información relevante contenida en la muestra.

El concepto de verosimilitud, formalizado a través de la función de verosimilitud, constituye otro fundamento crucial. Esta función mide la compatibilidad entre los datos observados y los posibles valores de los parámetros desconocidos. El principio de máxima verosimilitud, que selecciona como estimación aquellos valores paramétricos que maximizan esta función, proporciona un método general y potente para derivar estimadores con propiedades óptimas.

La estadística bayesiana introduce elementos adicionales como las distribuciones a priori y a posteriori, el teorema de Bayes y los métodos de integración numérica para aproximar distribuciones posteriores complejas. Este enfoque permite incorporar formalmente conocimiento previo en el proceso inferencial y actualizar nuestras creencias a la luz de nueva evidencia.

Ejemplos de Inferencia Estadística

La Inferencia Estadística cobra vida cuando se aplica a problemas reales. Estos ejemplos ilustran su versatilidad y relevancia práctica en diversos campos del conocimiento.

En epidemiología, los ensayos clínicos aleatorizados representan un ejemplo paradigmático. Cuando investigadores del Instituto Nacional de Salud evaluaron la eficacia de una vacuna contra el COVID-19, seleccionaron aleatoriamente a 40,000 participantes divididos en grupos de tratamiento y control. Los resultados mostraron una eficacia del 94% con un intervalo de confianza del 95% entre 89% y 97%. Esta inferencia permitió generalizar los hallazgos a la población general, fundamentando decisiones sanitarias cruciales a nivel mundial.

El ámbito económico también depende extensamente de métodos inferenciales. Consideremos el caso de un banco central que necesita estimar la tasa de inflación. Mediante un muestreo estratificado de precios de bienes y servicios en diferentes regiones, los economistas construyen índices de precios y calculan intervalos de confianza para la inflación real. Estas estimaciones influyen directamente en decisiones monetarias que afectan a toda la economía.

En las ciencias sociales, las encuestas de opinión pública ilustran perfectamente la inferencia estadística. Durante las elecciones presidenciales, las empresas demoscópicas entrevistan a aproximadamente 1,000-1,500 votantes potenciales para predecir resultados electorales que involucran a millones de ciudadanos. La precisión de estas predicciones, normalmente con márgenes de error de ±3%, demuestra el poder de la inferencia cuando se aplica correctamente.

La industria manufacturera emplea control estadístico de procesos, una aplicación sistemática de inferencia estadística. Una fábrica de semiconductores puede inspeccionar solo una pequeña fracción de sus chips (quizás 100 de cada 10,000) para inferir la tasa de defectos del lote completo. Si la proporción muestral de defectos excede cierto umbral, se detiene la producción para investigar posibles problemas.

Los estudios ecológicos frecuentemente utilizan métodos de captura-recaptura para estimar poblaciones animales. Al marcar y liberar un número conocido de individuos, y posteriormente observar la proporción de individuos marcados en una segunda captura, los biólogos pueden inferir el tamaño total de la población. Este método ha sido crucial para monitorear especies en peligro de extinción y establecer políticas de conservación efectivas.

Incluso en deportes encontramos aplicaciones sofisticadas. El análisis avanzado en baloncesto utiliza inferencia estadística para evaluar la contribución real de jugadores más allá de las estadísticas tradicionales. Mediante modelos lineales mixtos, se estima el impacto de cada jugador en la diferencia de puntuación, controlando factores como la calidad de compañeros y oponentes.

Pruebas de Hipótesis en la Inferencia Estadística

Las pruebas de hipótesis representan uno de los procedimientos más utilizados en la Inferencia Estadística, proporcionando un marco sistemático para tomar decisiones basadas en evidencia empírica. Este proceso sigue una estructura lógica comparable a un juicio donde la «presunción de inocencia» (hipótesis nula) se mantiene hasta que la evidencia en contra resulte suficientemente convincente.

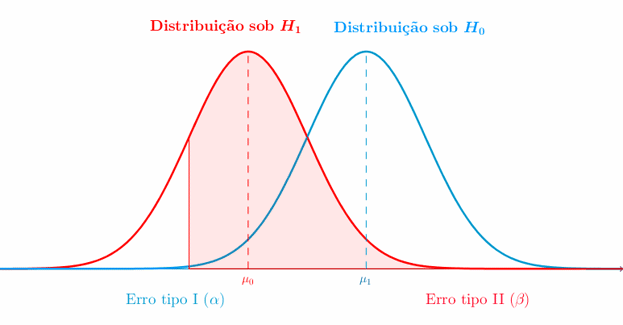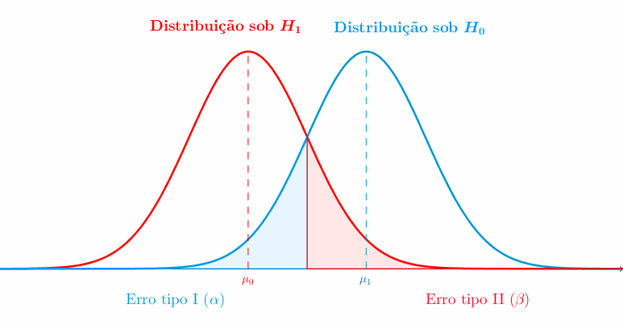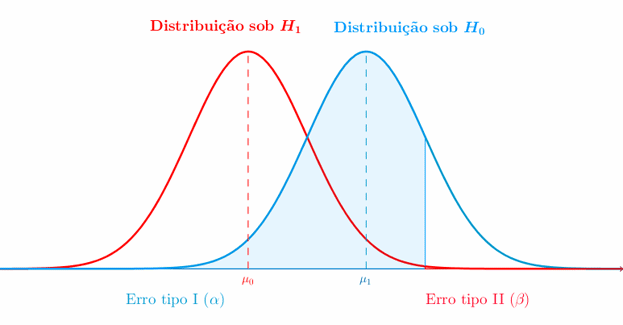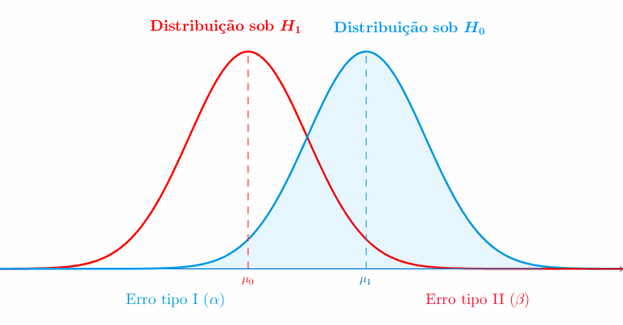
El procedimiento comienza con la formulación de dos hipótesis complementarias: la hipótesis nula (H₀) y la hipótesis alternativa (H₁). La primera representa típicamente la ausencia del efecto investigado o la igualdad entre parámetros, mientras que la segunda propone la existencia de dicho efecto o diferencia. Por ejemplo, al evaluar un nuevo medicamento, H₀ podría establecer que «el fármaco no es más efectivo que el placebo», mientras H₁ afirmaría lo contrario.

Una vez establecidas las hipótesis, se selecciona un estadístico de prueba apropiado. Este estadístico constituye una función matemática de los datos muestrales cuya distribución bajo H₀ es conocida. Dependiendo del contexto, podría tratarse de una prueba t, una prueba F, una prueba chi-cuadrado u otras alternativas.

El siguiente paso crucial consiste en determinar el nivel de significación (α), que representa la probabilidad máxima aceptable de cometer un error Tipo I (rechazar H₀ siendo verdadera). Convencionalmente se utilizan valores de 0.05 o 0.01, aunque esta elección debería fundamentarse en el contexto específico del estudio y en las consecuencias prácticas de los posibles errores.

Tras recolectar los datos, se calcula el valor del estadístico de prueba y se obtiene el valor p asociado. Este valor p representa la probabilidad de observar un resultado al menos tan extremo como el obtenido, asumiendo que H₀ es verdadera. Un valor p inferior a α conduce al rechazo de la hipótesis nula.

¿Qué significa realmente este rechazo? No implica necesariamente que H₀ sea falsa con certeza absoluta, sino que la evidencia empírica resulta suficientemente incompatible con ella según el criterio preestablecido. Esta distinción sutil pero fundamental subraya la naturaleza probabilística de la inferencia estadística.

Existen variantes importantes como las pruebas unilaterales (cuando el interés se centra exclusivamente en una dirección del efecto) y bilaterales (cuando ambas direcciones resultan relevantes). La potencia estadística, que representa la probabilidad de rechazar H₀ cuando realmente es falsa, constituye otro concepto esencial para evaluar la calidad de una prueba de hipótesis.

Intervalos de Confianza y su Interpretación

Los intervalos de confianza representan una de las herramientas más valiosas y frecuentemente mal interpretadas de la Inferencia Estadística. Proporcionan un rango de valores plausibles para un parámetro poblacional desconocido, junto con un nivel de confianza que cuantifica la fiabilidad de dicho rango.

Conceptualmente, un intervalo de confianza del 95% para un parámetro θ significa que, si repitiéramos el procedimiento de muestreo e intervalos indefinidamente, aproximadamente el 95% de los intervalos construidos contendrían el verdadero valor de θ. ¿Resulta contraintuitivo? Sin duda. La interpretación errónea más común consiste en afirmar que «existe un 95% de probabilidad de que el parámetro se encuentre dentro del intervalo calculado». Sin embargo, desde la perspectiva frecuentista, el parámetro es un valor fijo (aunque desconocido), no una variable aleatoria; la aleatoriedad reside en el intervalo, no en el parámetro.

La construcción de intervalos de confianza generalmente sigue una estructura matemática común:

Estimador puntual ± (Valor crítico × Error estándar del estimador)

Para una media poblacional, por ejemplo, utilizaríamos la media muestral como estimador puntual, y el valor crítico provendría de la distribución t de Student con n-1 grados de libertad (para muestras pequeñas) o de la distribución normal estándar (para muestras grandes).

La amplitud del intervalo refleja la precisión de nuestra estimación. Intervalos estrechos indican estimaciones precisas, mientras que intervalos amplios revelan mayor incertidumbre. Tres factores principales influyen en esta amplitud: el tamaño muestral (muestras mayores generalmente producen intervalos más estrechos), la variabilidad inherente en los datos (mayor variación produce intervalos más amplios) y el nivel de confianza seleccionado (niveles más altos generan intervalos más amplios).

Los intervalos de confianza ofrecen ventajas significativas frente a las pruebas de hipótesis tradicionales. Proporcionan información sobre la magnitud del efecto y su precisión, no simplemente sobre su significación estadística. Además, facilitan la meta-análisis y la comparación directa entre estudios.

En contextos aplicados, los intervalos de confianza adquieren interpretaciones prácticas valiosas. Un intervalo de confianza del 95% para el efecto de un tratamiento que oscila entre 5% y 15% de mejora indica no solo que el tratamiento probablemente sea efectivo (puesto que el intervalo excluye el cero), sino también que la magnitud del beneficio es clínicamente relevante incluso en su estimación más conservadora.

La interpretación bayesiana ofrece una alternativa: los intervalos de credibilidad sí permiten afirmar que «existe un 95% de probabilidad de que el parámetro se encuentre dentro del intervalo», puesto que en este marco conceptual los parámetros se consideran variables aleatorias.

Muestreo en la Inferencia Estadística

El muestreo constituye la piedra angular de la Inferencia Estadística, ya que la validez de cualquier conclusión inferencial depende críticamente de cómo se seleccionaron las observaciones que conforman la muestra. Esta fase, frecuentemente subestimada, resulta tan importante como los análisis sofisticados que la siguen.

El muestreo aleatorio simple representa el procedimiento más fundamental, donde cada elemento de la población tiene igual probabilidad de ser seleccionado. Imaginemos una urna con 10,000 bolas numeradas representando a todos los estudiantes de una universidad; extraer 500 bolas al azar ejemplificaría este método. Su principal ventaja radica en su sencillez teórica y en la posibilidad de calcular errores muestrales directamente. Sin embargo, puede resultar impracticable en poblaciones extensas o geográficamente dispersas.

El muestreo estratificado subdivide previamente la población en grupos homogéneos (estratos) según características relevantes como edad, género o nivel socioeconómico, realizando después un muestreo aleatorio dentro de cada estrato. Este enfoque garantiza la representatividad de todos los subgrupos significativos, especialmente cuando algunos son minoritarios pero relevantes para el estudio.

El muestreo por conglomerados selecciona inicialmente agrupaciones naturales (conglomerados) como distritos, escuelas o manzanas, y posteriormente muestrea elementos dentro de los conglomerados seleccionados. Resulta especialmente eficiente cuando la población está naturalmente agrupada y los costos de muestreo dependen principalmente de la dispersión geográfica.

El muestreo sistemático selecciona elementos a intervalos regulares después de un inicio aleatorio. Por ejemplo, en una lista de 10,000 clientes, podríamos seleccionar cada vigésimo cliente tras elegir aleatoriamente uno entre los primeros veinte. Este método combina la sencillez operativa con propiedades estadísticas generalmente satisfactorias, siempre que la lista no presente periodicidades que coincidan con el intervalo de selección.

La determinación del tamaño muestral óptimo representa una decisión crucial que equilibra precisión y costos. Fórmulas específicas permiten calcular este tamaño en función del error máximo admisible, el nivel de confianza deseado, la variabilidad poblacional y, en ocasiones, el efecto del diseño muestral.

Los errores muestrales, inevitables incluso en los diseños más cuidadosos, cuantifican la discrepancia esperable entre estadísticos muestrales y parámetros poblacionales debido exclusivamente al azar muestral. Separadamente, los errores no muestrales incluyen problemas como no respuesta, errores de medición o sesgos en el marco muestral, frecuentemente más perjudiciales que los errores muestrales pero más difíciles de cuantificar.

La teoría del muestreo demuestra matemáticamente que, bajo condiciones adecuadas, los estadísticos calculados a partir de muestras bien diseñadas convergen a los parámetros poblacionales conforme aumenta el tamaño muestral. Esta propiedad fundamental, derivada principalmente del teorema central del límite, sustenta la legitimidad científica de la inferencia estadística.

Aplicaciones Modernas de la Inferencia Estadística

La Inferencia Estadística, lejos de ser una disciplina estática, continúa evolucionando y expandiendo sus aplicaciones en la era digital. Las herramientas inferenciales clásicas se han adaptado y complementado con nuevos métodos para enfrentar los desafíos contemporáneos relacionados con la complejidad y volumen de los datos actuales.

En el ámbito del machine learning, los métodos de remuestreo como el bootstrap y la validación cruzada representan extensiones modernas de la inferencia estadística tradicional. Estas técnicas permiten estimar la variabilidad y el error de predicción de algoritmos complejos sin asumir distribuciones específicas. Por ejemplo, al entrenar un modelo de predicción de fraudes bancarios, la validación cruzada permite estimar su rendimiento futuro utilizando los datos disponibles de manera eficiente.

La genómica y otras ciencias ómicas han impulsado el desarrollo de métodos para manejar pruebas de hipótesis múltiples simultáneas. Cuando se analizan 20,000 genes para identificar aquellos asociados con una enfermedad, realizar 20,000 pruebas independientes al nivel usual de significación produciría numerosos falsos positivos. Métodos como Bonferroni, Benjamini-Hochberg o el control de la tasa de falsos descubrimientos (FDR) abordan este problema.

Los modelos jerárquicos bayesianos han encontrado aplicaciones sorprendentes en campos como la neuroimagen, donde permiten integrar información a diferentes niveles (vóxeles, regiones cerebrales, sujetos, grupos clínicos) mientras controlan apropiadamente la incertidumbre en cada nivel. Esta metodología ha revolucionado nuestra comprensión de trastornos neurológicos y psiquiátricos.

La inferencia causal, fundamentada en trabajos de Judea Pearl y Donald Rubin, extiende los métodos inferenciales tradicionales para abordar preguntas de causa-efecto, no meramente asociaciones. Utilizando herramientas como modelos de ecuaciones estructurales, grafos acíclicos dirigidos y métodos de emparejamiento, los investigadores pueden aproximarse a conclusiones causales incluso con datos observacionales, transformando campos como la epidemiología y la economía.

El análisis de datos espaciales y espacio-temporales incorpora dependencias geográficas en los modelos inferenciales. Métodos como los modelos autorregrivos condicionales (CAR) o los procesos gaussianos permiten inferir patrones espaciales en fenómenos tan diversos como la propagación de enfermedades infecciosas o la distribución de contaminantes ambientales.

Los métodos de inferencia aproximada como Approximate Bayesian Computation (ABC) o Likelihood-Free Inference posibilitan realizar inferencias en modelos complejos donde la función de verosimilitud resulta intratable. Estas técnicas han revolucionado campos como la genética de poblaciones, la cosmología y la modelación de sistemas complejos.

La integración de inferencia estadística con visualización interactiva de datos representa otra tendencia significativa. Herramientas como intervalos de confianza dinámicos, pruebas de permutación visuales o gráficos de inferencia bayesiana permiten a los usuarios explorar visualmente la incertidumbre en los datos y comprender intuitivamente conceptos inferenciales complejos.

Preguntas Frecuentes sobre Inferencia Estadística

1. ¿Cuál es la diferencia entre estadística descriptiva e inferencia estadística?

La estadística descriptiva se limita a resumir, organizar y presentar las características principales de un conjunto de datos mediante medidas numéricas (como medias o desviaciones estándar) y representaciones gráficas. La inferencia estadística va más allá: utiliza información muestral para obtener conclusiones sobre poblaciones enteras, cuantificando explícitamente la incertidumbre asociada a estas generalizaciones. Mientras la estadística descriptiva afirma «en esta muestra, la media es X», la inferencia estadística establece «basándonos en esta muestra, podemos estimar con un 95% de confianza que la media poblacional se encuentra entre A y B».

2. ¿Qué tamaño muestral necesito para realizar inferencias válidas?

No existe una respuesta universal, pues el tamaño muestral óptimo depende de múltiples factores: la variabilidad inherente al fenómeno estudiado, la precisión deseada, el tipo de inferencia (estimación o contraste), el nivel de confianza requerido y la estructura del diseño muestral. Fórmulas específicas permiten calcular tamaños muestrales para diferentes escenarios. Como principio general, muestras mayores proporcionan estimaciones más precisas, pero con rendimientos decrecientes. En algunos contextos, muestras de 30-50 elementos pueden resultar suficientes; en otros, se requieren cientos o miles de observaciones.

3. ¿Qué significa realmente un valor p de 0.05?

Un valor p de 0.05 indica que, si la hipótesis nula fuera cierta, la probabilidad de observar un resultado al menos tan extremo como el obtenido sería del 5%. Contrariamente a interpretaciones erróneas comunes, NO representa: la probabilidad de que la hipótesis nula sea cierta, la probabilidad de obtener el mismo resultado si repitiéramos el experimento, ni un indicador directo de la importancia práctica del hallazgo. El umbral convencional de 0.05 para la significación estadística constituye una convención, no una verdad matemática inmutable.

4. ¿Por qué las muestras deben ser aleatorias para realizar inferencias válidas?

La aleatoriedad en el muestreo garantiza que cada elemento poblacional tenga una probabilidad conocida y no nula de ser seleccionado, eliminando sesgos sistemáticos en la selección. Esta propiedad resulta fundamental porque los métodos inferenciales basan sus propiedades matemáticas (distribuciones muestrales, errores estándar, etc.) en esta aleatoriedad. Sin ella, las fórmulas estadísticas convencionales pierden validez y las inferencias resultantes pueden conducir a conclusiones erróneas, independientemente del tamaño muestral o la sofisticación analítica posterior.

5. ¿Cuándo debo utilizar métodos paramétricos y cuándo no paramétricos?

Los métodos paramétricos asumen que los datos siguen distribuciones específicas (frecuentemente la normal) y realizan inferencias sobre parámetros de dichas distribuciones. Resultan apropiados cuando los supuestos distribucionales se cumplen razonablemente, ofreciendo mayor potencia estadística. Los métodos no paramétricos hacen supuestos mínimos sobre las distribuciones subyacentes, basándose en rankings u otras propiedades ordinales de los datos. Son preferibles cuando las distribuciones se alejan significativamente de la normalidad, contienen valores atípicos influyentes o las escalas de medición son ordinales más que continuas.

6. ¿La significación estadística implica relevancia práctica?

No necesariamente. La significación estadística únicamente indica que los resultados observados difícilmente podrían atribuirse al azar muestral bajo la hipótesis nula. Con muestras suficientemente grandes, efectos minúsculos y prácticamente irrelevantes pueden alcanzar significación estadística. La evaluación de la relevancia práctica requiere considerar la magnitud del efecto, su precisión (intervalos de confianza) y su importancia en el contexto específico de aplicación. Un tratamiento médico estadísticamente significativo pero con efectos clínicos marginales podría carecer de relevancia práctica real.

Conclusión

La Inferencia Estadística constituye una herramienta intelectual extraordinariamente potente que ha transformado nuestra capacidad para extraer conocimiento válido a partir de datos incompletos. Su marco conceptual nos permite navegar sistemáticamente entre lo particular y lo general, cuantificando explícitamente el grado de incertidumbre inherente a nuestras conclusiones.

A lo largo de este recorrido, hemos explorado sus fundamentos matemáticos, sus metodologías principales y sus aplicaciones en diversos campos del conocimiento. Hemos visto cómo las pruebas de hipótesis y los intervalos de confianza ofrecen aproximaciones complementarias para responder preguntas científicas. También hemos destacado la importancia crucial del muestreo adecuado como condición previa para cualquier inferencia válida.

Las aplicaciones modernas demuestran la continua relevancia y adaptabilidad de esta disciplina, que ha evolucionado para enfrentar los desafíos contemporáneos relacionados con la complejidad y volumen de datos en la era digital. Desde el machine learning hasta la genómica, la inferencia estadística sigue proporcionando el rigor metodológico necesario para extraer conclusiones confiables.

Sin embargo, como toda herramienta poderosa, requiere un uso responsable y consciente de sus limitaciones. Las interpretaciones erróneas de conceptos como valores p, intervalos de confianza o significación estadística pueden conducir a conclusiones científicas equivocadas con potenciales consecuencias prácticas graves.