Prueba de hipótesis: concepto y pasos a seguir

La prueba de hipótesis es una herramienta fundamental en el ámbito de la investigación científica y estadística. Permite evaluar la validez de una afirmación o suposición sobre una población o un fenómeno en particular. Al realizar esta prueba de manera adecuada, los investigadores pueden obtener conclusiones significativas y confiables. En este artículo, estudiaremos en detalle el concepto de la prueba de hipótesis, los pasos que se deben seguir para llevarla a cabo y su importancia en la toma de decisiones basadas en evidencia.

Prueba de hipótesis: concepto y definición

La prueba de hipótesis es un procedimiento estadístico que se utiliza para evaluar la veracidad de una afirmación o suposición sobre una población o fenómeno. Se basa en la recolección y análisis de datos muestrales para determinar si los resultados obtenidos respaldan o contradicen la hipótesis planteada.

Para comprender mejor el concepto de la prueba de hipótesis, es importante tener claridad sobre algunos términos clave:

1. Población y muestra

La población se refiere al conjunto completo de elementos que se desea investigar. Por ejemplo, si estamos interesados en conocer el promedio de edad de todos los estudiantes de una universidad en particular, la población estaría compuesta por todos los estudiantes de esa institución.

Por otro lado, la muestra es un subconjunto representativo de la población que se selecciona para realizar el estudio. En el ejemplo anterior, podríamos seleccionar una muestra de 100 estudiantes para obtener datos y hacer inferencias sobre la población completa.

2. Hipótesis nula y alternativa

En la prueba de hipótesis, se plantean dos hipótesis: la hipótesis nula (H0) y la hipótesis alternativa (H1).

• La hipótesis nula (H0) es la afirmación inicial que se pretende poner a prueba. Es la suposición que se sostiene hasta que haya evidencia suficiente para rechazarla. Por ejemplo, en el caso de la edad promedio de los estudiantes, la hipótesis nula podría ser que el promedio de edad es igual a 22 años.
• La hipótesis alternativa (H1), por otro lado, es la afirmación que se sostiene si hay suficiente evidencia para rechazar la hipótesis nula. En nuestro ejemplo, la hipótesis alternativa podría ser que el promedio de edad no es igual a 22 años.

3. Nivel de significancia

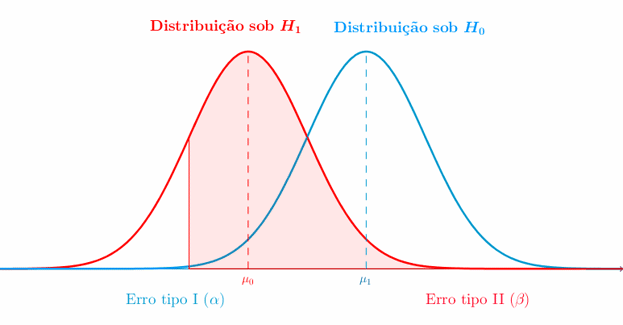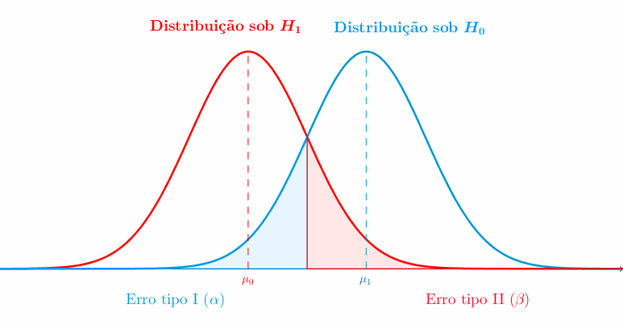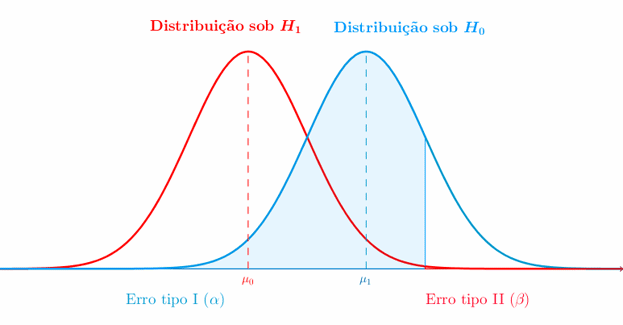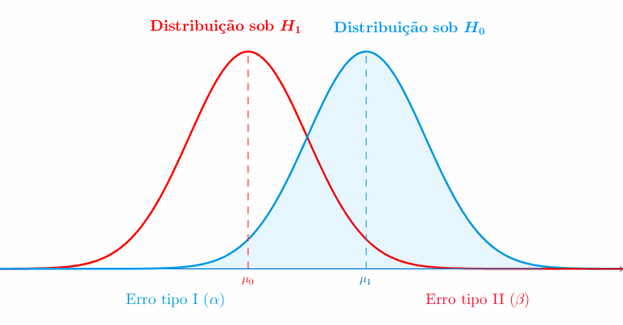
El nivel de significancia (α) es el umbral establecido para determinar si los resultados obtenidos son lo suficientemente extremos como para rechazar la hipótesis nula. Comúnmente, se utiliza un nivel de significancia del 5% (α = 0.05). Esto implica que si la probabilidad de obtener los resultados observados o más extremos bajo la hipótesis nula es menor al 5%, se rechaza la hipótesis nula.

Pasos a seguir en la prueba de hipótesis

La prueba de hipótesis sigue un proceso estructurado que consta de varios pasos. A continuación, detallaremos cada uno de ellos:

Paso 1: Formular las hipótesis

El primer paso en la prueba de hipótesis es formular claramente la hipótesis nula (H0) y la hipótesis alternativa (H1) en función de los objetivos de investigación y los datos disponibles. Es importante que estas hipótesis sean mutuamente excluyentes y colectivamente exhaustivas.

Paso 2: Determinar el nivel de significancia

En este paso, se establece el nivel de significancia (α) que se utilizará para evaluar los resultados. Como se mencionó anteriormente, el nivel de significancia comúnmente utilizado es del 5% (α = 0.05). Sin embargo, en algunos casos, se puede elegir un nivel de significancia más bajo para aumentar la rigurosidad de la prueba.

Paso 3: Recolectar datos y calcular estadísticos

Una vez establecidas las hipótesis y el nivel de significancia, se procede a recolectar una muestra representativa de la población en estudio. Es importante utilizar métodos de muestreo adecuados para garantizar la representatividad de la muestra.

Luego, se calculan los estadísticos necesarios para llevar a cabo la prueba de hipótesis. Esto puede variar dependiendo del tipo de datos y el diseño del estudio. Algunos estadísticos comunes utilizados incluyen la media, la proporción, la desviación estándar y la correlación, entre otros.

Paso 4: Determinar la región crítica y calcular el valor p

En este paso, se determina la región crítica, que corresponde a los valores extremos que llevarían al rechazo de la hipótesis nula. La región crítica está determinada por el nivel de significancia establecido previamente.

Además, se calcula el valor p, que representa la probabilidad de obtener los resultados observados o más extremos bajo la hipótesis nula. Si el valor p es menor que el nivel de significancia, se rechaza la hipótesis nula.

Paso 5: Tomar una decisión y sacar conclusiones

En este paso, se toma una decisión basada en los resultados obtenidos en la prueba de hipótesis. Si el valor p es menor que el nivel de significancia, se rechaza la hipótesis nula y se acepta la hipótesis alternativa. En caso contrario, no se tiene suficiente evidencia para rechazar la hipótesis nula y se concluye que los datos no proporcionan pruebas significativas en contra de ella.

Paso 6: Comunicar los resultados

El último paso consiste en comunicar de manera clara y precisa los resultados obtenidos en la prueba de hipótesis. Esto implica describir las hipótesis planteadas, los datos recolectados, los estadísticos utilizados, el valor p obtenido y las conclusiones alcanzadas. Es fundamental presentar los resultados de manera transparente para que otros investigadores puedan evaluar y replicar el estudio.

Preguntas frecuentes sobre la prueba de hipótesis

Aquí tienes algunas preguntas frecuentes sobre la prueba de hipótesis, junto con sus respuestas:

1. ¿Qué sucede si no se sigue correctamente el proceso de la prueba de hipótesis?Si no se sigue adecuadamente el proceso de la prueba de hipótesis, los resultados obtenidos pueden carecer de validez y no proporcionar conclusiones confiables. Es fundamental seguir cada uno de los pasos mencionados anteriormente para garantizar la rigurosidad y la objetividad de la prueba.
2. ¿Cuál es la importancia de la prueba de hipótesis en la investigación científica?La prueba de hipótesis desempeña un papel crucial en la investigación científica, ya que permite evaluar la validez de las suposiciones y afirmaciones sobre una población o fenómeno en particular. Al obtener resultados significativos, los investigadores pueden tomar decisiones fundamentadas y generar conocimientos confiables en sus respectivas áreas de estudio.
3. ¿Existen diferentes tipos de pruebas de hipótesis?Sí, existen diferentes tipos de pruebas de hipótesis, que varían según el tipo de datos y el diseño del estudio. Algunos ejemplos comunes incluyen la prueba t de Student, la prueba de chi-cuadrado, la prueba ANOVA y la prueba de correlación, entre otras. Cada tipo de prueba se adapta a situaciones específicas y tiene sus propias suposiciones y requisitos.
4. ¿Qué sucede si no se rechaza la hipótesis nula?Si no se rechaza la hipótesis nula, significa que los datos no proporcionan suficiente evidencia para contradecir la afirmación inicial. Sin embargo, esto no implica necesariamente que la hipótesis nula sea verdadera. Puede haber otras explicaciones o factores que influyan en los resultados obtenidos.
5. ¿Qué sucede si se rechaza incorrectamente la hipótesis nula?Si se rechaza incorrectamente la hipótesis nula, se comete un error conocido como “falso positivo” o error de tipo I. Esto implica concluir que existe una diferencia o efecto cuando en realidad no lo hay. Es importante tener en cuenta el nivel de significancia establecido para controlar la probabilidad de cometer este tipo de errores.
6. ¿Es posible probar todas las hipótesis utilizando la prueba de hipótesis?No, la prueba de hipótesis tiene limitaciones y no es aplicable a todas las situaciones. Algunas hipótesis pueden ser difíciles de probar debido a la falta de datos adecuados o la complejidad del fenómeno en estudio. En tales casos, es necesario utilizar otros métodos de investigación o considerar enfoques alternativos.

Conclusión de Prueba de hipótesis

La prueba de hipótesis es una herramienta valiosa para evaluar la validez de las afirmaciones y suposiciones en la investigación científica y estadística. Siguiendo los pasos adecuados, los investigadores pueden obtener resultados significativos y confiables que respalden la toma de decisiones basada en evidencia.

En este artículo, hemos analizado el concepto de la prueba de hipótesis, los pasos que se deben seguir para llevarla a cabo y su importancia en la investigación. Esperamos que esta información te haya proporcionado una comprensión sólida de este tema fundamental. ¡Ahora estás listo para aplicar la prueba de hipótesis en tus propias investigaciones!