Qué es la regresión lineal y cómo se utiliza en estadística
En el campo de la estadística y el análisis de datos, la regresión lineal es una técnica fundamental que permite modelar y analizar la relación entre variables. Es ampliamente utilizada en diversos campos, desde la economía hasta la biología, pasando por la sociología y la psicología. En este artículo, descubriremos en detalle qué es la regresión lineal y cómo se utiliza en estadística. Te guiaremos a través de los conceptos clave, los pasos para aplicarla y su relevancia en la interpretación de datos. ¡Prepárate para adentrarte en el fascinante mundo de la regresión lineal!
Contenido
- Qué es la regresión lineal y cómo se utiliza en estadística
- Los conceptos básicos de la regresión lineal
- La importancia de la regresión lineal en estadística
- Pasos para aplicar la regresión lineal
- Supuestos de la regresión lineal
- ¿Cuándo se utiliza la regresión lineal?
- Ventajas y desventajas de la regresión lineal
- ¿Cuáles son las diferencias entre regresión lineal simple y múltiple?
- ¿Qué es el coeficiente de determinación (R²)?
- ¿Cómo se interpreta el coeficiente de determinación?
- ¿Qué es el error estándar de la estimación?
- ¿Qué son los residuos en la regresión?
- ¿Qué son los valores atípicos y cómo afectan la regresión lineal?
- ¿Cómo se pueden mejorar los resultados de la regresión?
- ¿Cuáles son algunas aplicaciones comunes de la regresión lineal?
- La regresión lineal en la vida cotidiana
- Conclusión sobre qué es la regresión lineal
- Preguntas frecuentes sobre qué es la regresión lineal
Qué es la regresión lineal y cómo se utiliza en estadística
La regresión lineal es una técnica estadística utilizada para modelar la relación entre una variable dependiente y una o más variables independientes. En su forma más básica, asume una relación lineal entre estas variables, lo que significa que los cambios en las variables independientes se pueden predecir mediante una función lineal de la variable dependiente. Esta técnica es valiosa para comprender cómo los cambios en una variable se relacionan con los cambios en otras variables y para predecir valores futuros.
Los conceptos básicos de la regresión lineal
En la regresión lineal, hay varios conceptos clave que es importante comprender:
- Variable dependiente: También conocida como variable de respuesta o variable objetivo, es la variable que se intenta predecir o modelar utilizando las variables independientes.
- Variables independientes: También llamadas variables predictoras o covariables, son las variables utilizadas para predecir o explicar la variabilidad de la variable dependiente.
- Relación lineal: En la regresión lineal, se asume que la relación entre las variables dependientes e independientes es lineal, es decir, puede representarse mediante una línea recta en un gráfico.
- Coeficientes de regresión: Son los valores que representan la pendiente y el punto de intersección de la línea de regresión. Estos coeficientes se calculan durante el proceso de ajuste del modelo y permiten estimar los valores de la variable dependiente en función de las variables independientes.
La importancia de la regresión lineal en estadística
La regresión lineal desempeña un papel fundamental en la estadística y el análisis de datos. A través de esta técnica, los investigadores pueden:
- Identificar la relación entre variables: La regresión lineal permite determinar si existe una relación significativa entre una variable dependiente y una o más variables independientes.
- Predecir valores futuros: Al ajustar un modelo de regresión lineal, es posible utilizarlo para hacer predicciones sobre el valor de la variable dependiente en función de los valores de las variables independientes.
- Evaluar el impacto de variables independientes: La regresión lineal proporciona información sobre la contribución relativa de las variables independientes en la predicción de la variable dependiente.
- Realizar análisis de tendencias: Al trazar la línea de regresión, se puede identificar la dirección y la intensidad de la relación entre las variables, lo que ayuda a comprender las tendencias y patrones en los datos.
Pasos para aplicar la regresión lineal
La aplicación efectiva de la regresión lineal requiere seguir una serie de pasos bien definidos. A continuación, detallaremos cada uno de estos pasos:
Recopilación de datos y preparación
Antes de realizar cualquier análisis de regresión lineal, es crucial recopilar los datos relevantes y prepararlos adecuadamente. Esto implica:
- Definir las variables: Identifica y nombra la variable dependiente y las variables independientes que se utilizarán en el análisis.
- Recopilar los datos: Reúne los datos necesarios para todas las variables involucradas en el análisis. Esto puede implicar la realización de encuestas, la recopilación de datos históricos u obtener información de bases de datos existentes.
- Limpieza de datos: Verifica si los datos recopilados contienen errores, valores atípicos o datos faltantes. Realiza las correcciones o eliminaciones necesarias para asegurar la calidad de los datos.
Identificación y selección de variables
Una vez que los datos están preparados, el siguiente paso es identificar y seleccionar las variables que serán incluidas en el modelo de regresión lineal. Esto implica:
- Exploración de datos: Analiza los datos mediante gráficos, medidas de resumen y técnicas de visualización para comprender la relación entre las variables.
- Análisis de correlación: Calcula las correlaciones entre la variable dependiente y las variables independientes para identificar las relaciones más fuertes.
- Selección de variables: Basándote en la exploración y el análisis de correlación, selecciona las variables independientes que tienen una relación significativa con la variable dependiente.
Análisis de la relación lineal
Una vez seleccionadas las variables, es importante analizar la relación lineal entre la variable dependiente y las variables independientes. Esto se puede hacer de varias maneras:
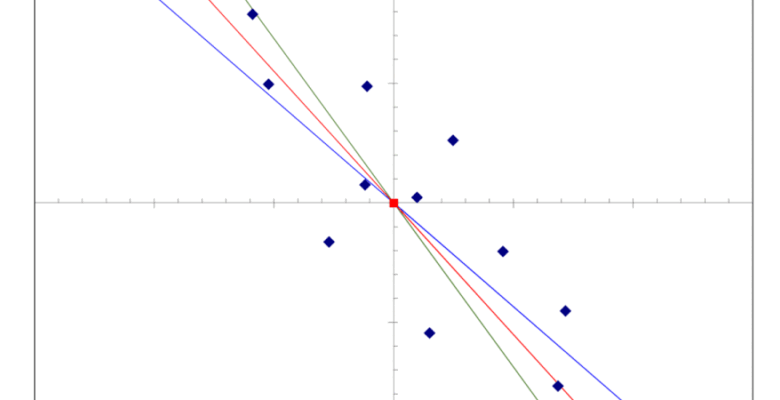
- Diagrama de dispersión: Crea un diagrama de dispersión para visualizar la relación entre la variable dependiente y cada una de las variables independientes.
- Análisis de correlación: Calcula los coeficientes de correlación para medir la fuerza y la dirección de la relación lineal.
- Gráficos de regresión: Realiza gráficos de regresión para visualizar la línea de mejor ajuste entre la variable dependiente y las variables independientes.
Ajuste del modelo de regresión lineal
Una vez que se ha establecido una relación lineal entre las variables, es hora de ajustar el modelo de regresión lineal. Esto implica:
- Elección del tipo de regresión: Determina si utilizarás una regresión lineal simple (una variable independiente) o una regresión lineal múltiple (múltiples variables independientes).
- Cálculo de los coeficientes de regresión: Utiliza técnicas estadísticas para calcular los coeficientes de regresión que definen la línea de regresión.
- Evaluación de la calidad del ajuste: Analiza medidas como el coeficiente de determinación (R²) y el error estándar de la estimación para evaluar qué tan bien se ajusta el modelo a los datos.
Evaluación y validación del modelo
Después de ajustar el modelo, es importante evaluar su validez y realizar validaciones adicionales. Esto incluye:
- Pruebas de hipótesis: Realiza pruebas estadísticas para evaluar si los coeficientes de regresión son significativamente diferentes de cero.
- Validación cruzada: Divide los datos en conjuntos de entrenamiento y prueba para evaluar el rendimiento del modelo en datos no utilizados durante el ajuste.
- Análisis de residuos: Examina los residuos del modelo para verificar si cumplen con los supuestos de la regresión lineal.
Interpretación de los resultados
Una vez validado el modelo, llega el momento de interpretar los resultados obtenidos. Esto implica:
- Interpretación de los coeficientes: Analiza los coeficientes de regresión para entender cómo influyen las variables independientes en la variable dependiente.
- Coeficiente de determinación (R²): Evalúa el R² para determinar qué proporción de la variabilidad de la variable dependiente es explicada por el modelo de regresión lineal.
- Significancia estadística: Evalúa la significancia estadística de los coeficientes de regresión para determinar si las variables independientes tienen un efecto significativo en la variable dependiente.
Supuestos de la regresión lineal
La regresión lineal se basa en ciertos supuestos que deben cumplirse para obtener resultados válidos. Estos supuestos incluyen:
- Linealidad: La relación entre las variables debe ser lineal, es decir, se puede representar mediante una línea recta en un gráfico.
- Homocedasticidad: La varianza de los residuos debe ser constante en todos los niveles de las variables independientes.
- Independencia de los residuos: Los residuos no deben mostrar patrones sistemáticos o correlaciones entre sí.
- Normalidad: Los residuos deben seguir una distribución normal.
- Ausencia de multicolinealidad: Las variables independientes deben ser independientes entre sí y no mostrar una alta correlación.
¿Cuándo se utiliza la regresión lineal?
La regresión lineal se utiliza en una amplia gama de contextos y situaciones. Algunos ejemplos de su aplicación incluyen:
- Estimación de ventas futuras en función de variables como el gasto en publicidad, el precio de los productos y el tamaño del mercado.
- Análisis de la relación entre el nivel educativo y el salario en una población determinada.
- Predicción del rendimiento académico de los estudiantes en función de variables como el tiempo de estudio, las horas de sueño y el consumo de cafeína.
- Estimación de la demanda de un producto en función de su precio y las características del mercado.
- Análisis de la relación entre la edad y la presión arterial en una muestra de pacientes.
Ventajas y desventajas de la regresión lineal
La regresión tiene ventajas y desventajas que debemos tener en cuenta al utilizar esta técnica:
Ventajas:
- Simplicidad: La regresión lineal es relativamente fácil de entender y aplicar, lo que la hace accesible incluso para personas sin un conocimiento estadístico profundo.
- Interpretación intuitiva: Los coeficientes de regresión tienen una interpretación directa y pueden explicar cómo afecta cada variable independiente a la variable dependiente.
- Predicciones lineales: La regresión lineal permite hacer predicciones utilizando una función lineal, lo que facilita la interpretación de los resultados y la comunicación de los hallazgos.
Desventajas:
- Supuestos requeridos: La regresión lineal se basa en varios supuestos que pueden no cumplirse en todos los casos. Si los supuestos no se cumplen, los resultados pueden ser poco confiables o incorrectos.
- Relaciones no lineales: Si la relación entre las variables no es lineal, la regresión lineal puede producir resultados inadecuados o sesgados.
- Sensibilidad a valores atípicos: Los valores atípicos pueden tener un impacto significativo en los resultados de la regresión lineal, distorsionando los coeficientes y las predicciones.
¿Cuáles son las diferencias entre regresión lineal simple y múltiple?
La regresión lineal se puede dividir en dos categorías principales: regresión lineal simple y regresión lineal múltiple.
- Regresión lineal simple: En la regresión lineal simple, se utiliza una única variable independiente para predecir la variable dependiente. La relación entre las variables se representa mediante una línea recta en un gráfico bidimensional. La fórmula general de la regresión lineal simple es: Y = β₀ + β₁X + ε, donde Y representa la variable dependiente, X la variable independiente, β₀ y β₁ los coeficientes de regresión y ε el término de error.
- Regresión lineal múltiple: En la regresión lineal múltiple, se utilizan dos o más variables independientes para predecir la variable dependiente. La relación entre las variables se representa mediante un hiperplano en un espacio multidimensional. La fórmula general de la regresión lineal múltiple es: Y = β₀ + β₁X₁ + β₂X₂ + … + βₚXₚ + ε, donde Y representa la variable dependiente, X₁, X₂, …, Xₚ las variables independientes, β₀, β₁, β₂, …, βₚ los coeficientes de regresión y ε el término de error.
En resumen, la regresión lineal simple se utiliza cuando solo se tiene una variable independiente, mientras que la regresión lineal múltiple se utiliza cuando hay dos o más variables independientes que influyen en la variable dependiente.
¿Qué es el coeficiente de determinación (R²)?
El coeficiente de determinación, comúnmente denotado como R², es una medida estadística que indica qué tan bien se ajusta el modelo de regresión lineal a los datos observados. R² proporciona una medida de la proporción de la variabilidad de la variable dependiente que se puede explicar por el modelo de regresión lineal.
R² varía de 0 a 1, donde:
- R² = 0 indica que el modelo no explica ninguna variabilidad de la variable dependiente.
- R² = 1 indica que el modelo explica toda la variabilidad de la variable dependiente.
En otras palabras, cuanto más cerca esté R² de 1, mejor se ajusta el modelo a los datos observados. Sin embargo, es importante tener en cuenta que un valor alto de R² no garantiza la causalidad entre las variables o la precisión de las predicciones.
¿Cómo se interpreta el coeficiente de determinación?
La interpretación del coeficiente de determinación (R²) se puede resumir de la siguiente manera:
- R² = 0: El modelo no explica ninguna variabilidad de la variable dependiente. Las variables independientes no tienen relación lineal con la variable dependiente.
- 0 < R² < 1: El modelo explica parte de la variabilidad de la variable dependiente. Un valor más alto indica que el modelo tiene un mejor ajuste a los datos observados.
- R² = 1: El modelo explica toda la variabilidad de la variable dependiente. El modelo se ajusta perfectamente a los datos observados.
Es importante recordar que el coeficiente de determinación no indica la dirección o la magnitud de la relación entre las variables. Simplemente proporciona una medida de qué tan bien se ajusta el modelo de regresión lineal a los datos.
¿Qué es el error estándar de la estimación?
El error estándar de la estimación (SEE, por sus siglas en inglés) es una medida de la dispersión de los datos alrededor de la línea de regresión. Representa la desviación estándar promedio de los residuos del modelo de regresión lineal.
El SEE se utiliza para evaluar la precisión del modelo y es especialmente útil cuando se comparan diferentes modelos de regresión. Un valor más bajo de SEE indica que los datos se ajustan de manera más cercana a la línea de regresión y que el modelo tiene un mejor ajuste.
La interpretación del SEE depende de las unidades de la variable dependiente. En general, cuanto menor sea el SEE, mejor será la capacidad del modelo para predecir los valores de la variable dependiente.
¿Qué son los residuos en la regresión?
Los residuos en la regresión lineal son las diferencias entre los valores observados de la variable dependiente y los valores predichos por el modelo de regresión lineal. Representan la discrepancia entre los datos reales y los datos estimados por la línea de regresión.
Los residuos pueden ser positivos o negativos, dependiendo de si los valores observados están por encima o por debajo de la línea de regresión. Idealmente, los residuos deben distribuirse aleatoriamente alrededor de cero y no mostrar ningún patrón sistemático.
El análisis de los residuos es importante para verificar si se cumplen los supuestos de la regresión y evaluar la calidad del modelo. Si los residuos muestran un patrón sistemático o una correlación entre sí, puede indicar que el modelo no se ajusta adecuadamente a los datos.
¿Qué son los valores atípicos y cómo afectan la regresión lineal?
Los valores atípicos, también conocidos como outliers, son observaciones que difieren significativamente del patrón general de los datos. Estos valores pueden ser extremadamente altos o bajos en comparación con los demás puntos de datos.
Los valores atípicos pueden tener un impacto significativo en la regresión lineal, ya que pueden influir en los coeficientes de regresión y distorsionar la línea de regresión. Esto se debe a que la regresión lineal minimiza la suma de los residuos al cuadrado, lo que significa que los valores atípicos con residuos grandes pueden tener un peso desproporcionado en el ajuste del modelo.
Es importante identificar y evaluar los valores atípicos antes de realizar un análisis de regresión lineal. Si se identifican valores atípicos, se pueden considerar diferentes enfoques, como eliminarlos del análisis o utilizar técnicas robustas de regresión que sean menos sensibles a los valores atípicos.
¿Cómo se pueden mejorar los resultados de la regresión?
Para mejorar los resultados de la regresión lineal, se pueden considerar varias estrategias:
- Transformación de variables: Si los datos no cumplen con los supuestos de la regresión lineal, se pueden aplicar transformaciones a las variables para lograr una relación más lineal. Por ejemplo, se pueden aplicar logaritmos o raíces cuadradas a las variables.
- Inclusión de variables adicionales: Si el modelo inicial no explica suficiente variabilidad, se pueden incluir variables adicionales que puedan estar relacionadas con la variable dependiente.
- Eliminación de valores atípicos: Los valores atípicos pueden afectar el ajuste del modelo. Si se identifican valores atípicos, se puede considerar eliminarlos del análisis o utilizar técnicas robustas de regresión.
- Validación cruzada: Realizar validación cruzada para evaluar el rendimiento del modelo en datos no utilizados durante el ajuste. Esto ayuda a verificar si el modelo se ajusta bien a nuevos datos y no está sobreajustado.
- Considerar otras técnicas de regresión: Si la relación entre las variables no es lineal, se pueden explorar otras técnicas de regresión, como la regresión no lineal o los modelos de aprendizaje automático.
¿Cuáles son algunas aplicaciones comunes de la regresión lineal?
La regresión lineal se utiliza ampliamente en una variedad de campos y aplicaciones. Algunas de las aplicaciones comunes incluyen:
- Economía: En economía, se utiliza la regresión lineal para modelar y predecir variables como la demanda de productos, el crecimiento económico y los precios de los activos financieros.
- Ciencias sociales: En campos como la sociología y la psicología, la regresión lineal se utiliza para analizar la relación entre variables sociales y psicológicas, como la relación entre la educación y los ingresos o la relación entre el estrés y la salud mental.
- Biología: En biología, la regresión lineal se utiliza para estudiar la relación entre variables biológicas, como la relación entre la edad y el rendimiento físico o la relación entre la dosis de un fármaco y la respuesta biológica.
- Marketing: En marketing, la regresión lineal se utiliza para modelar y predecir variables como las ventas, el comportamiento del consumidor y el impacto de las estrategias de marketing.
- Investigación médica: En investigación médica, la regresión lineal se utiliza para analizar la relación entre variables médicas, como la relación entre la presión arterial y los factores de riesgo cardiovascular o la relación entre el peso y la altura en el crecimiento infantil.
La regresión lineal en la vida cotidiana
La regresión lineal también tiene aplicaciones en la vida cotidiana. Aunque a menudo no nos damos cuenta, podemos encontrar ejemplos de regresión lineal en situaciones comunes, como:
- Previsión del tiempo: Los modelos meteorológicos utilizan técnicas de regresión lineal para predecir el clima en función de variables como la presión atmosférica, la temperatura y la humedad.
- Predicción de precios inmobiliarios: Los modelos de regresión lineal se utilizan para predecir los precios de las viviendas en función de variables como el tamaño de la propiedad, la ubicación y las características.
- Análisis de deportes: En el análisis deportivo, la regresión lineal se utiliza para evaluar el rendimiento de los atletas en función de variables como el tiempo de entrenamiento, la edad y las habilidades físicas.
- Estimación de gastos: La regresión lineal puede utilizarse para estimar gastos mensuales, como facturas de servicios públicos, en función de variables como el número de personas en el hogar o la temperatura promedio.
La regresión lineal es una herramienta versátil que puede aplicarse en numerosos contextos y situaciones de la vida cotidiana.
Conclusión sobre qué es la regresión lineal
Qué es la regresión lineal. La regresión lineal es una técnica fundamental en el campo de la estadística y el análisis de datos. Permite modelar y analizar la relación entre variables, proporcionando una base sólida para la predicción y la interpretación de datos. En este artículo, hemos explorado los conceptos básicos de la regresión lineal, los pasos para aplicarla y su importancia en la estadística. Hemos discutido los supuestos, ventajas y desventajas, y hemos proporcionado ejemplos de aplicaciones comunes.
Recuerda que es una herramienta poderosa, pero su interpretación adecuada requiere comprender los supuestos y limitaciones asociados. Siempre es recomendable analizar los resultados con precaución y considerar otros métodos o técnicas si los supuestos no se cumplen o los resultados no son satisfactorios.
Preguntas frecuentes sobre qué es la regresión lineal
1. ¿Cuál es la diferencia entre la regresión lineal simple y la regresión lineal múltiple? En la regresión lineal simple se utiliza una única variable independiente, mientras que en la regresión lineal múltiple se utilizan dos o más variables independientes para predecir la variable dependiente.
2. ¿Cómo se interpreta el coeficiente de determinación (R²)? El coeficiente de determinación (R²) indica qué proporción de la variabilidad de la variable dependiente se puede explicar por el modelo de regresión lineal. Un valor de R² cercano a 1 indica que el modelo se ajusta bien a los datos observados.
3. ¿Qué son los residuos en la regresión lineal? Los residuos son las diferencias entre los valores observados de la variable dependiente y los valores predichos por el modelo de regresión lineal. Representan la discrepancia entre los datos reales y los datos estimados por la línea de regresión.
4. ¿Qué son los valores atípicos y cómo afectan la regresión lineal? Los valores atípicos, también conocidos como outliers, son observaciones que difieren significativamente del patrón general de los datos. Los valores atípicos pueden tener un impacto significativo en la regresión lineal, ya que pueden influir en los coeficientes de regresión y distorsionar la línea de regresión.
5. ¿Cómo se pueden mejorar los resultados de la regresión lineal? Se pueden considerar estrategias como la transformación de variables, la inclusión de variables adicionales, la eliminación de valores atípicos, la validación cruzada y la exploración de otras técnicas de regresión.
6. ¿Cuáles son algunas aplicaciones comunes de la regresión lineal? Se utiliza en una amplia variedad de campos y aplicaciones, como economía, ciencias sociales, biología, marketing e investigación médica, entre otros.