Fractales en la Vida Cotidiana

Los fractales son estructuras geométricas que se repiten a diferentes escalas y son omnipresentes en la naturaleza y en nuestras vidas diarias. A menudo, sin darnos cuenta, interactuamos con estas fascinantes formas que nos rodean. Desde la estructura de los árboles hasta el diseño de las ciudades, los fractales juegan un papel crucial. Este artículo explorará cómo los fractales en la vida cotidiana influyen en diversas áreas y nos ayudarán a entender mejor nuestro entorno.

Además casi al final del artículo mostramos un ejemplo básico de fractal en Pyhton y su salida: El Triángulo de Sierpinski, completamente explicando su funcionalidad y el código fuente. Al mismo tiempo que proporcionamos la versión Free Pascal.

Fractales en la Vida Cotidiana

Los fractales en la vida cotidiana son más comunes de lo que podríamos imaginar. Estos patrones geométricos complejos y autosimilares pueden encontrarse en una variedad de contextos y aplicaciones que nos afectan directamente. Desde las formas naturales hasta las innovaciones tecnológicas, los fractales nos rodean y enriquecen nuestra percepción del mundo.

Introducción a los Fractales

Definición y Concepto de Fractales

Los fractales son estructuras que se caracterizan por la repetición de un patrón a diferentes escalas. Esta autosimilitud puede observarse en objetos naturales como montañas, costas y nubes. La geometría fractal, un concepto matemático desarrollado por Benoît Mandelbrot en los años 70, ha revelado cómo estas formas aparentemente caóticas siguen leyes matemáticas precisas.

Matemáticas de los Fractales

Geometría Fractal

La geometría fractal estudia las propiedades y comportamientos de los fractales. Utilizando ecuaciones matemáticas, podemos modelar y entender cómo los fractales se forman y evolucionan. Esto ha permitido avances significativos en diversos campos, desde la computación gráfica hasta la biología.

Historia de los Fractales

Pioneros y Descubrimientos Clave

El concepto de fractales ha sido explorado por muchos matemáticos y científicos a lo largo de la historia. Benoît Mandelbrot es quizás el más conocido por popularizar el término, pero figuras como Gaston Julia y Georg Cantor también hicieron contribuciones importantes. Estos descubrimientos han abierto nuevas perspectivas en la comprensión de la naturaleza y las matemáticas.

Fractales en la Naturaleza

Ejemplos en Flora y Fauna

Los fractales son abundantes en la naturaleza. Desde la estructura de los helechos hasta las conchas de los caracoles, los patrones fractales pueden observarse en una amplia variedad de organismos vivos. Estos patrones no solo son estéticamente agradables, sino que también tienen funciones biológicas esenciales, como la maximización de la eficiencia y la resiliencia.

Fractales en la Ciencia

Aplicaciones en Física y Biología

En la ciencia, los fractales tienen múltiples aplicaciones. En física, se utilizan para modelar sistemas complejos y caóticos. En biología, ayudan a entender la estructura de organismos vivos y procesos naturales. Por ejemplo, la estructura de los pulmones humanos y los sistemas vasculares siguen patrones fractales que optimizan el intercambio de gases y la circulación sanguínea.

Fractales en la Tecnología

Uso en Computación y Diseño de Software

La tecnología ha aprovechado los fractales para mejorar diversos aspectos del diseño y la computación. Los algoritmos fractales se utilizan en la creación de gráficos por computadora, permitiendo generar paisajes y texturas realistas. Además, en el diseño de software, los fractales pueden optimizar la eficiencia de los algoritmos y la gestión de datos.

Fractales en la vida cotidiana: Medicina

Diagnóstico y Tratamiento de Enfermedades

La medicina ha encontrado en los fractales una herramienta valiosa para el diagnóstico y tratamiento de enfermedades. Las imágenes médicas, como las resonancias magnéticas y las tomografías, utilizan conceptos fractales para analizar y visualizar estructuras corporales complejas. Esto ha permitido avances en la detección temprana de enfermedades y en la planificación de tratamientos más efectivos.

Fractales en la Arquitectura

Diseño de Edificios y Estructuras

La arquitectura ha incorporado patrones fractales para crear diseños innovadores y eficientes. Los edificios que utilizan geometría fractal no solo son visualmente impactantes, sino que también pueden mejorar la distribución del espacio y la eficiencia energética. Ejemplos de esto pueden verse en estructuras icónicas alrededor del mundo que combinan estética y funcionalidad.

Fractales en el Arte

Obras de Arte y Música

El arte ha explorado los fractales como una fuente de inspiración creativa. Las obras de arte fractal utilizan algoritmos matemáticos para crear imágenes y formas visualmente impresionantes. En la música, los fractales se han utilizado para componer piezas con estructuras rítmicas y melódicas complejas que resuenan con la naturaleza fractal del sonido.

Fractales en la Economía

Modelos Económicos y Mercados Financieros

Los fractales también han encontrado aplicaciones en la economía. Los modelos fractales se utilizan para analizar y predecir el comportamiento de los mercados financieros, ayudando a identificar patrones y tendencias que no son visibles mediante métodos tradicionales. Esto ha llevado a una mejor comprensión de la dinámica del mercado y a estrategias de inversión más informadas.

Fractales en el Clima

Patrones Meteorológicos y Modelos Climáticos

El estudio de los patrones meteorológicos y climáticos ha beneficiado enormemente de la geometría fractal. Los modelos fractales permiten analizar la complejidad del clima y predecir fenómenos como huracanes y patrones de lluvia con mayor precisión. Esto es crucial para la planificación y mitigación de desastres naturales.

Fractales en la Educación

Enseñanza y Comprensión de Conceptos Complejos

En la educación, los fractales se utilizan para enseñar conceptos complejos de una manera visual y accesible. Los estudiantes pueden entender mejor las matemáticas y las ciencias naturales al observar y crear fractales, lo que facilita la comprensión de temas abstractos y fomenta el pensamiento crítico y creativo.

Fractales en la vida cotidiana: Diseño Gráfico

Creación de Imágenes y Animaciones

El diseño gráfico ha adoptado los fractales para crear imágenes y animaciones innovadoras. Los programas de diseño utilizan algoritmos fractales para generar gráficos complejos y visualmente atractivos, que pueden aplicarse en publicidad, cine, y videojuegos, entre otros campos.

Fractales en la Literatura

Narrativas y Estructuras Textuales

La literatura también ha explorado el uso de estructuras fractales en la narrativa. Autores y poetas han utilizado patrones repetitivos y autosimilares para construir historias y poemas que reflejan la naturaleza fractal del pensamiento y la experiencia humana.

Fractales en la Música

Composición y Ritmos Fractales

En la música, los fractales se utilizan para crear composiciones con ritmos y estructuras complejas. Esto permite a los compositores experimentar con nuevas formas de expresión y crear piezas musicales que resuenan con la complejidad y belleza de los patrones naturales.

Fractales en la Agricultura

Optimización de Cultivos y Recursos

La agricultura ha aplicado conceptos fractales para optimizar la producción de cultivos y el uso de recursos. Al analizar los patrones de crecimiento de las plantas y la distribución de los nutrientes, los agricultores pueden mejorar la eficiencia y sostenibilidad de sus prácticas agrícolas.

Fractales en la Gastronomía

Presentación y Texturas de Alimentos

La gastronomía ha incorporado los fractales en la presentación y creación de texturas de alimentos. Los chefs utilizan patrones fractales para diseñar platos visualmente atractivos y crear experiencias gastronómicas únicas, explorando nuevas dimensiones de sabor y estética.

Fractales en la Psicología

Percepción y Cognición Humana

En psicología, los fractales se estudian para entender mejor la percepción y la cognición humana. Los patrones fractales pueden influir en nuestra percepción del entorno y en cómo procesamos la información, lo que tiene implicaciones para el diseño de entornos y la terapia cognitiva.

Fractales en la Ecología

Conservación y Gestión Ambiental

La ecología ha adoptado los fractales para estudiar y gestionar los ecosistemas. Al comprender los patrones fractales en la distribución de las especies y la estructura de los hábitats, los ecologistas pueden desarrollar estrategias más efectivas para la conservación y la gestión sostenible del medio ambiente.

Tipos de fractales en la vida cotidiana

Existen varios tipos de fractales que se clasifican según sus características geométricas y propiedades matemáticas. Aquí te explico brevemente algunos de los tipos más comunes:

1. Fractales Deterministas: Estos fractales se generan mediante algoritmos deterministas y su forma se repite exactamente a diferentes escalas. Ejemplos incluyen el conjunto de Mandelbrot y el triángulo de Sierpinski.
2. Fractales Estocásticos: A diferencia de los deterministas, los fractales estocásticos muestran variabilidad en su forma y estructura debido a factores aleatorios. Son útiles para modelar fenómenos naturales complejos como la textura de las nubes.
3. Fractales IFS (Sistemas de Funciones Iteradas): Se generan mediante la repetición de un conjunto de funciones matemáticas aplicadas a puntos específicos en el espacio. Son utilizados en la generación de paisajes y gráficos por computadora.
4. Fractales Geométricos: Estos fractales tienen una estructura definida y regular, como los conjuntos de Julia y los fractales de Newton, que se basan en métodos geométricos para su construcción.
5. Fractales de L-systems: Utilizan sistemas de reescritura para modelar el crecimiento de plantas y estructuras biológicas. Son ampliamente utilizados en biología y modelado de vegetación.

Estos tipos de fractales muestran la diversidad y la versatilidad de estas formas geométricas, que se encuentran en la naturaleza y tienen aplicaciones en numerosos campos científicos y creativos.

Ejemplos del fractal del Triángulo de Sierpinski en Python y Free Pascal

Este código implementa el Triángulo de Sierpinski en Python utilizando la biblioteca turtle y su versión Free Pascal usando la unidad Graph. El programa emplea recursión para dibujar este fascinante fractal, dividiendo repetidamente triángulos en subtriángulos más pequeños. La implementación en Python ofrece una visualización colorida y dinámica del fractal, demostrando cómo patrones complejos pueden surgir de reglas simples aplicadas iterativamente.

Diferencias con la versión en FreePascal:

1. Accesibilidad: El código Python utiliza la biblioteca turtle, que viene incluida en la instalación estándar, mientras que la versión FreePascal requiere configuración adicional de la unidad Graph.
2. Visualización: La versión Python ofrece una representación más colorida, usando diferentes colores para cada nivel de recursión. La versión FreePascal típicamente usa un solo color.
3. Interfaz gráfica: Turtle en Python proporciona una interfaz gráfica más sencilla y moderna comparada con la unidad Graph de FreePascal.
4. Sintaxis y estructura: El código Python tiende a ser más conciso y legible para principiantes, mientras que FreePascal puede parecer más verbose y estructurado.
5. Ejecución: El programa Python se ejecuta en un entorno interpretado, ofreciendo resultados inmediatos, mientras que el código FreePascal necesita ser compilado antes de la ejecución.

Ambas implementaciones demuestran efectivamente los conceptos de recursión y fractales, pero la versión Python resulta más accesible y visualmente atractiva para aquellos que se inician en la programación gráfica y los fractales.

1. Ejemplo de Fractal: El Triángulo de Sierpinski en Python

Aquí tenemos una versión equivalente del programa del Triángulo de Sierpinski en Python. Este programa utiliza la biblioteca turtle para dibujar, que es una manera sencilla de crear gráficos en Python:

import turtle  # Importamos la biblioteca turtle para dibujar

def draw_triangle(points, color, my_turtle):
    """
    Dibuja un triángulo relleno dado tres puntos y un color.
    """
    my_turtle.fillcolor(color)  # Establece <a class="wpil_keyword_link" href="https://ciberlinea.net/la-psicologia-del-color-en-el-marketing/"   title="el color" data-wpil-keyword-link="linked"  data-wpil-monitor-id="1332">el color</a> de relleno
    my_turtle.up()  # Levanta el lápiz
    my_turtle.goto(points[0][0], points[0][1])  # Va al primer punto
    my_turtle.down()  # Baja el lápiz para dibujar
    my_turtle.begin_fill()  # Comienza a rellenar
    my_turtle.goto(points[1][0], points[1][1])  # Va al segundo punto
    my_turtle.goto(points[2][0], points[2][1])  # Va al tercer punto
    my_turtle.goto(points[0][0], points[0][1])  # Vuelve al primer punto
    my_turtle.end_fill()  # Termina de rellenar

def get_mid(p1, p2):
    &amp;quot;&amp;quot;&amp;quot;
    Calcula el punto medio entre dos puntos.
    &amp;quot;&amp;quot;&amp;quot;
    return ((p1[0] + p2[0]) / 2, (p1[1] + p2[1]) / 2)

def sierpinski(points, degree, my_turtle):
    &amp;quot;&amp;quot;&amp;quot;
    Dibuja el Triángulo de Sierpinski de forma recursiva.
    &amp;quot;&amp;quot;&amp;quot;
    colors = [&amp;#039;blue&amp;#039;, &amp;#039;red&amp;#039;, &amp;#039;green&amp;#039;, &amp;#039;white&amp;#039;, &amp;#039;yellow&amp;#039;, &amp;#039;violet&amp;#039;, &amp;#039;orange&amp;#039;]
    draw_triangle(points, colors[degree], my_turtle)  # Dibuja el triángulo actual
    if degree &amp;amp;gt; 0:  # Si aún no hemos llegado al nivel base de recursión
        # Dibuja los tres sub-triángulos
        sierpinski([points[0],
                    get_mid(points[0], points[1]),
                    get_mid(points[0], points[2])],
                   degree-1, my_turtle)
        sierpinski([points[1],
                    get_mid(points[0], points[1]),
                    get_mid(points[1], points[2])],
                   degree-1, my_turtle)
        sierpinski([points[2],
                    get_mid(points[2], points[1]),
                    get_mid(points[0], points[2])],
                   degree-1, my_turtle)

def main():
    &amp;quot;&amp;quot;&amp;quot;
    Función principal que configura el entorno y inicia el dibujo.
    &amp;quot;&amp;quot;&amp;quot;
    my_turtle = turtle.Turtle()
    my_turtle.speed(&amp;#039;fastest&amp;#039;)  # Configura la velocidad de dibujo al máximo
    my_win = turtle.Screen()  # Crea una ventana para dibujar
    my_points = [(-300, -150), (0, 300), (300, -150)]  # Puntos del triángulo inicial
    sierpinski(my_points, 5, my_turtle)  # Comienza a dibujar con profundidad 5
    my_win.exitonclick()  # Mantiene la ventana abierta hasta que se haga clic

if __name__ == &amp;#039;__main__&amp;#039;:
    main()

Resultado de ejecución

Funcionamiento del código:

Ahora, explicaré cómo funciona este programa de manera clara:

1. El programa utiliza la biblioteca turtle para dibujar. Esta biblioteca simula una tortuga que se mueve por la pantalla dejando un rastro, lo que permite crear gráficos de manera sencilla.
2. La función draw_triangle dibuja un solo triángulo relleno. Toma tres puntos y un color, mueve la «tortuga» a cada punto y rellena el área resultante.
3. La función get_mid calcula el punto medio entre dos puntos dados. Esto es crucial para dividir los triángulos en sub-triángulos.
4. La función sierpinski es el corazón del programa. Funciona de manera recursiva:
   • Primero, dibuja el triángulo actual.
   • Luego, si aún no hemos llegado al nivel base de recursión (cuando degree es 0), divide el triángulo en tres sub-triángulos y llama a sí misma para cada uno de estos sub-triángulos.
   • Cada nivel de recursión usa un color diferente, creando un efecto visual interesante.
5. La función main configura el entorno de dibujo:
   • Crea una «tortuga» y una ventana de dibujo.
   • Define los puntos del triángulo inicial grande.
   • Inicia el proceso de dibujo llamando a sierpinski con una profundidad de 5.
   • Mantiene la ventana abierta hasta que el usuario haga clic en ella.
6. El bloque if __name__ == '__main__': asegura que main() solo se ejecute si este script se está ejecutando directamente, no si se está importando como un módulo.

En resumen, este programa crea el Triángulo de Sierpinski dividiendo repetidamente triángulos en sub-triángulos más pequeños. La recursión permite que este proceso se repita hasta alcanzar el nivel de detalle deseado, creando así el patrón fractal característico del Triángulo de Sierpinski.

2. Ejemplo de Fractal: El triángulo de Sierpinski en Free Pascal

El Triángulo de Sierpinski es un fractal simple pero fascinante. Se crea dividiendo repetidamente un triángulo en triángulos más pequeños y eliminando el central. Este proceso se repite indefinidamente, creando un patrón intrincado de autosimilaridad.

El código en FreePascal que veremos a continuación implementa este fractal utilizando recursión. Dibuja el Triángulo de Sierpinski en modo gráfico, permitiendo visualizar cómo una serie de instrucciones sencillas puede generar una estructura compleja. Este ejemplo no solo ilustra conceptos fractales, sino que también demuestra el poder de la recursión en programación.

program SierpinskiTriangle;
uses Graph;  // Importa la unidad gráfica para dibujar

// Procedimiento para dibujar un triángulo simple
procedure DrawTriangle(x1, y1, x2, y2, x3, y3: SmallInt);
begin
  Line(x1, y1, x2, y2);  // Dibuja la primera línea del triángulo
  Line(x2, y2, x3, y3);  // Dibuja la segunda línea del triángulo
  Line(x3, y3, x1, y1);  // Dibuja la tercera línea del triángulo
end;

// Procedimiento recursivo para dibujar el triángulo de Sierpinski
procedure Sierpinski(x1, y1, x2, y2, x3, y3: SmallInt; depth: Integer);
var
  mx1, my1, mx2, my2, mx3, my3: SmallInt;  // Puntos medios de los lados
begin
  if depth = 0 then
    DrawTriangle(x1, y1, x2, y2, x3, y3)  // Si la profundidad es 0, dibuja el triángulo
  else
  begin
    // Calcula los puntos medios de los lados del triángulo
    mx1 := (x1 + x2) div 2;
    my1 := (y1 + y2) div 2;
    mx2 := (x2 + x3) div 2;
    my2 := (y2 + y3) div 2;
    mx3 := (x3 + x1) div 2;
    my3 := (y3 + y1) div 2;

    // Llama recursivamente a Sierpinski para los tres subtriángulos
    Sierpinski(x1, y1, mx1, my1, mx3, my3, depth - 1);
    Sierpinski(mx1, my1, x2, y2, mx2, my2, depth - 1);
    Sierpinski(mx3, my3, mx2, my2, x3, y3, depth - 1);
  end;
end;

var
  gd, gm: SmallInt;  // Variables para el modo gráfico
  maxX, maxY: SmallInt;  // Dimensiones máximas de la pantalla
begin
  gd := Detect;  // Detecta el controlador gráfico
  InitGraph(gd, gm, '');  // Inicia el modo gráfico

  // Verifica si se inició correctamente el modo gráfico
  if GraphResult <> grOk then
  begin
    Writeln('Error al iniciar el modo gráfico');
    Halt(1);
  end;

  maxX := GetMaxX;  // Obtiene el ancho máximo de la pantalla
  maxY := GetMaxY;  // Obtiene el alto máximo de la pantalla

  // Dibuja el triángulo de Sierpinski
  Sierpinski(10, maxY - 10, maxX - 10, maxY - 10, maxX div 2, 10, 7);

  ReadLn;  // Espera a que el usuario presione Enter
  CloseGraph;  // Cierra el modo gráfico
end.

Resultado de ejecución

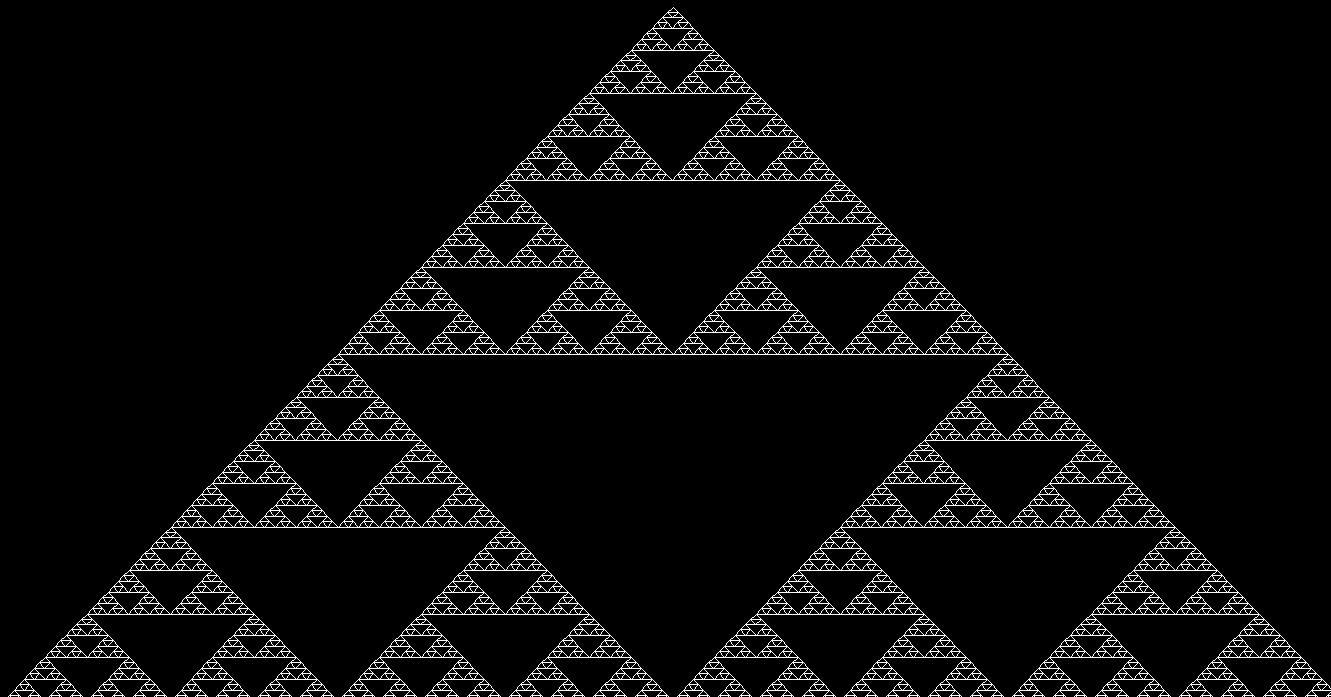
Funcionamiento del código:

1. El programa dibuja un fractal conocido como el Triángulo de Sierpinski. Este es un patrón geométrico que se crea dividiendo repetidamente un triángulo en triángulos más pequeños.

2. Utiliza recursión para crear el patrón. La idea básica es:

– Empezar con un triángulo grande.
– Dividir este triángulo en cuatro triángulos más pequeños conectando los puntos medios de los lados.
– Eliminar (o en este caso, no dibujar) el triángulo central.
– Repetir este proceso para los tres triángulos restantes.

3. El procedimiento `DrawTriangle` simplemente dibuja un triángulo conectando tres puntos.

4. El corazón del programa está en el procedimiento `Sierpinski`. Este es recursivo y funciona así:

– Si la profundidad (`depth`) llega a 0, dibuja un triángulo simple.
– Si no, calcula los puntos medios de los lados del triángulo actual.
– Luego, llama a sí mismo tres veces, una para cada subtriángulo, reduciendo la profundidad en 1.

5. En el programa principal:

– Se inicializa el modo gráfico.
– Se obtienen las dimensiones máximas de la pantalla.
– Se llama a `Sierpinski` con los puntos que definen un triángulo grande que ocupa casi toda la pantalla, y una profundidad inicial de 7.

6. El resultado visual es un patrón intrincado de triángulos dentro de triángulos, donde el nivel de detalle depende de la profundidad especificada (en este caso, 7).

Este programa es un excelente ejemplo de cómo los conceptos matemáticos complejos, como los fractales, pueden ser implementados de manera relativamente simple utilizando la recursión en programación.

Preguntas Frecuentes: Fractales en la Vida Cotidiana

¿Qué es un fractal?

Un fractal es una estructura geométrica que se repite a diferentes escalas, mostrando patrones autosimilares.

¿Cómo se aplican los fractales en la tecnología?

Los fractales se utilizan en el diseño de gráficos por computadora y en la optimización de algoritmos y datos en el desarrollo de software.

¿Qué ejemplos de fractales existen en la naturaleza?

Ejemplos incluyen la estructura de los helechos, las conchas de los caracoles, y las ramas de los árboles.

¿Cómo ayudan los fractales en la medicina?

Los fractales se utilizan en imágenes médicas para analizar estructuras corporales complejas y mejorar el diagnóstico y tratamiento de enfermedades.

¿Cuál es la importancia de los fractales en la arquitectura?

La geometría fractal en la arquitectura ayuda a crear diseños innovadores y eficientes, mejorando la distribución del espacio y la eficiencia energética.

¿Cómo se utilizan los fractales en la música?

En la música, los fractales se utilizan para crear composiciones con ritmos y estructuras complejas, explorando nuevas formas de expresión musical.

Conclusión y Reflexión: Fractales en la Vida Cotidiana

En conclusión, los fractales en la vida cotidiana son una prueba de la profunda interconexión entre las matemáticas, la naturaleza y nuestras actividades diarias. Estos patrones no solo nos rodean, sino que también influyen en la manera en que entendemos y interactuamos con el mundo.

Desde la ciencia hasta el arte, los fractales han demostrado ser una herramienta invaluable para explorar y comprender la complejidad de nuestro entorno. La investigación y la aplicación de los fractales continúan evolucionando, prometiendo nuevos descubrimientos y avances en múltiples disciplinas.